Temptation. Sometimes it’s fine to yield. I stumbled on a math problem while writing the entry for TGRWT #5 and I can’t solve it. What is the most efficient way to cut diamond shapes from a square?

Making the cut

Baklava and kibbeh are usually cut into diamond shapes, which is a little harder to do than squares or rectangles. My mom eyeballs her way through a zig-zag patterns. The perfectionist in me wants to get some edible inks to print a guide for the knife to follow. Or better, a computer controlled laser cutter. In the mean time, there is an alternative to mom’s pattern (and other cooks too) that gives more full diamonds from a square dish:

You baked it in a square dish, right?

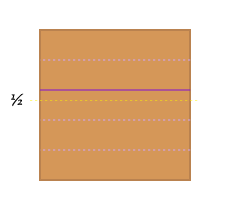
Start out by dividing the square in five horizontal strips. Eyeball the middle (yellow line) and then move the knife up a bit. The idea is to get a strip that will be divided into two and another that will be divided into three.

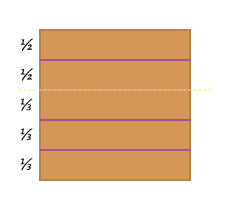
Finish the horizontal cuts by dividing the upper section into two and the lower into three.

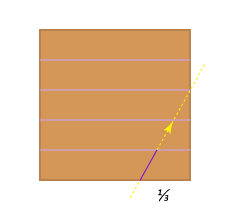
Move one third from the right and aim at the second cut down. Make one small cut.

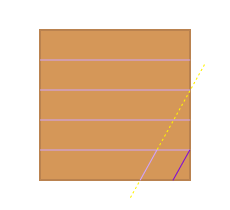
Make one piece to the right of that cut by cutting the strip parallel to the first angled cut.

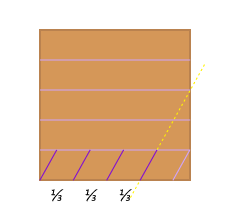
Divide the other side into three pieces.

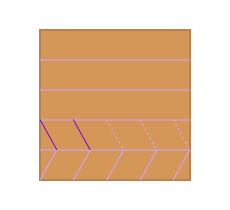
Using the first strip as a guide zig-zag your way through the rest of the square.

Finish the pattern, one row at a time.

The pattern is based on the idea that we can eyeball halves and thirds quite well. So to get fifths one tries to build it up from halves and thirds.

Mathematics. Beware

The zig-zag pattern has more full pieces than the straight line pattern.

You have the equivalent of 2.8 pieces of left-overs in the zig-zag, whereas in the straight line its 4.5 pieces. Which is better depends on how much you have to serve and how much you want to nibble.

That closet mathematician in me keeps asking what is the most efficient pattern? And if one finds it, how does one prove it is the most efficient? Finite space tiling questions are usually hard. Most efficient means that the area of the wasted pieces is as small as possible. The pieces would be perfect 60 degree lozenges of side one and not the 60.95 degree described above. The wasted pieces should add up to an area that is small with respect to the perimeter of the square (and not the area, because for simple patterns such as the zig-zag pattern the ratio of wastage to total area goes to zero as the square gets bigger).

This problem seems beyond recreational mathematics and in the realm of interacting models in statistical mechanics.